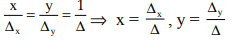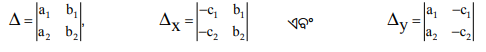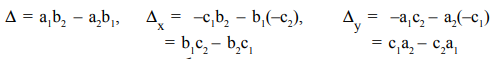Algebra ବୀଜଗଣିତ Exercise-1(B) ସରଳ ସହସମୀକରଣର ସମାଧାନ Solution to Linear Simultaneous Equation Class 10th Odia

Theory Note, Formulas, Solution Note and Quiz of Algebra Exercise – 1 (B) Class 10th Odia

Substitution Method ପ୍ରତିକଳ୍ପନ ପଦ୍ଧତି

• ଯେକୌଣସି ଏକ ସମୀକରଣକୁ ସଜାଡି x କୁ y ମାଧ୍ୟମରେ(ବା y କୁ x ମାଧ୍ୟମରେ) ପ୍ରକାଶ କରିବା
• Rearrange one of the given equations to express x in terms of y
• ଏବେ y ରୂପରେ ଥିବା x ର ମାନକୁ ଦ୍ଵିତୀୟ ସମୀକରଣରେ ବ୍ୟବହାର କଲେ ଆମେ y ର ପାଇଁ ସମୀକରଣକୁ ସମାଧାନ କରିପାରିବା
• Now, the expression for x can be substituted in the other equation to find the value of y.
• ଏବେ y ର ମାନକୁ ପ୍ରଥମ ସମୀକରଣରେ ବ୍ୟବହାର କାଲେ x ର ମାନ ନିର୍ଣ୍ଣୟ କରିହେବ ।
• Finally, substitute the value of y in any of the equations to find the value of x.

ଉଦାହରଣ

3x – 4y = 0 (i)

9x – 8y = 12 (ii)

• Step 1 : ସମୀକରଣ (i)ରେ x କୁ y ରୂପରେ ପ୍ରକାଶ କରିବା
• 3x = 4y
• =>x = 4/3 y
• Step 2 : x ର ମାନକୁ ସମୀକରଣ (ii)ରେ ବ୍ୟବହାର କରିବା
• 9 (4/3)y – 8y = 12
• =>12y – 8y = 12
• => 4y = 12
• => y = 3
• Step 3 : y ର ମନକୁ ସମୀକରଣ (i) ରେ ବ୍ୟବହାର କରି x ପାଇଁ ସମାଧାନ କରିବା
• x = 4/3y
• => x = 4/3 (3) = 4

x, y ର ମାନ ପ୍ରତିକଳ୍ପନ ପଦ୍ଧତିରେ ଆମେ 4,3 ପାଇଲୁ

Elimination Method ଅପସାରଣ ପଦ୍ଧତି

• ଦୁଇଟି ସମୀକରଣର ଯେ କୌଣସି ଏକ ଅଜ୍ଞାତରଶୀର ସହଗକୁ ସମାନ କରିବା ପାଇଁ ଉଭୟ ସମୀକରଣକୁ ଏକ ସଂଖ୍ୟା ସହ ଗୁଣିବା ।
• Multiply the given equations by a constant, so as to make the coefficients of any one of the variables in the equations equal.
• ଏବେ ସମୀକରଣ ଦ୍ୱୟକୁ ଯୋଗ ବା ବିୟୋଗ କରି ସମସହଗ ଥିବା ଅଜ୍ଞାତରଶୀକୁ ଅପସାରଣ କରିବା
• Add or subtract the equations to eliminate the variable having the same coefficients.
• ଏବେ କେବଳ ଗୋଟିଏ ଅଜ୍ଞତାରଶୀ ପାଇଁ ସମୀକରଣକୁ ସମାଧାନ କରିବା
• Now, solve the equation for one variable.
• ମିଳିଥିବା ସମାଧାନକୁ ଯେକୌଣସି ସମୀକରଣରେ ପ୍ରୟୋଗ କରି ଅନ୍ୟ ଅଜ୍ଞାତରଶୀର ସମାଧାନ ପାଇ ପାରିବା
• Substitute the variable value in any of the equations to find the value of the other variable.

ଉଦାହରଣ

ସମାଧାନ କର

2x + 3y – 8 = 0 (i)

3x + y – 5 = 0 ()

• 3x(ii) =>9x +3y-15 = 0
• (ii) – (i) 9x-2x+3y-3y-15-(-8) = 0
• =>7x-7= 0
• => x = 1 …….. (iii)

• put x=1in (ii)
• 3 (1) + y -5 = 0
• => y = 5-3 = 2

(x,y) = (1,2)

Cross Multiplication ବଜ୍ର ଗୁଣନ

ଯଦି ଦୁଇଟି ସରଳସହସମୀକରଣ a₁x + b₁ y +c₁ = 0 ଏବଂ a₂x + b₂ y +c₂ = 0 ହୁଅନ୍ତି ତେବେ ବଜ୍ରଗୁଣନ ସୂତ୍ର ଅନୁସାରେ ତାଙ୍କ ସମାଧାନ

If two linear Simultaneous Equations are a₁x + b₁ y +c₁ = 0 and a₂x + b₂ y +c₂ = 0 then the solution is

x = (b₁c₂ – b₂c₁) / (a₁b₂ – a₂b₁)

y =(c₁a₂ – c₂a₁) / (a₁b₂ -a₂b₁)

Important ଦ୍ରଷ୍ଟବ୍ୟ

• ଯଦି c₁ = c₂ = 0 ଏବଂ a₁b₂ -a₂b₁ ≠ 0 ହେଲେ ସମୀକରଣ ଦ୍ୱୟର ସମାଧାନ (0,0) ହେବ । ସମୀକରଣ ଦ୍ୱୟଙ୍କୁ ସମସହସମୀକରଣ କୁହାଯିବ ।
• If c₁ = c₂ = 0 and a₁b₂ -a₂b₁ ≠ 0 , then the solution of the two equation is (0,0) । The two equations are said to be Homogenuous Simultaneous Equation.

Example ଉଦାହରଣ

ସମାଧାନ କରିବା 2x – 3y –1 = 0, 4x + y – 9 = 0

ଏଠାରେ a1 = 2, b1 = -3, c1 = -1, a2 = 4, b2 = 1, c2 = -9

x = (b₁c₂ – b₂c₁) / (a₁b₂ – a₂b₁)

• = (-3)(-9) – 1(-1) / 2.1 – 4(-3)
• = 27+1/ 2+12 = 28/14

• => x = 2

y =(c₁a₂ – c₂a₁) / (a₁b₂ -a₂b₁)

• = (-1)4 -(-9)2 / 2.1 – 4(-3)
• = -4+18/14 = 14/14
• => y = 1

Cramer’s Rule

ବଜ୍ର ଗୁଣନ ହିଁ Cramer’s Rule.

Cross multiplication formula is based on Cramer’s Rule.

Solution Note and Quiz